The apothecary's balance
I spend too much time thinking instead of sleeping, but I run across such gems. For example, I recently lost sleep when I realized that my naive idea of how an apothecary’s balance worked was wrong. It seemed simple: a symmetric crosspiece pivoting on a strong, heaving base, with mass hanging from each end. The difference in weight determines the angle. Except that it doesn’t.
If we load both sides of the balance equally, what happens? Gravity acting on the mass on each side of the balance exerts a constant force straight down at the point where it is attached. When the crosspiece is level, the force is perpendicular to it and acts to rotate it around the pivot.

If the crosspiece is tilted, then the part of the force perpendicular to it still acts to rotate it, but the rest pushes on the pivot.
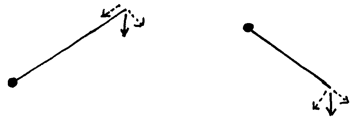
The closer the angle between force and crosspiece is to a right angle, the stronger the rotational force. When the mass is attached to the crosspiece, the perpendicular force is the same on both sides no matter how tilted the crosspiece is
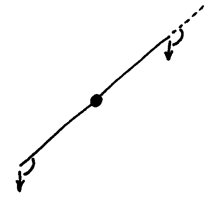
and rotation from each mass balances that from the other. It’s a seesaw, which anyone who has spent time in a playground knows you can leave at any angle you desire. It doesn’t describe a balance.
I lay awake for I don’t know how long envisioning every balance I could remember. What had I missed? There are incredibly simple balances: a base supporting a pivot and a simple crossbar. They differed from the idealization above in only one thing: I had never seen a balance with the weight suspended from a hole through the crosspiece. It was always attached at least to an eyelet underneath, if not to some ornate structure below the crosspiece.
This wasn’t the first thing that caught my attention, but as soon as it did, I had a flash of geometry, and knew that I had the answer. Geometric insight doesn’t actually arrive in pictures but in a combination of touch and motion and half glimpsed sketches, but this is more or less what appeared to me
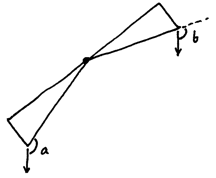
along with the fact that angles a and b are different. The components perpendicular to the line connecting the pivot and the point where the force is exerted are different. Angle b is closer to a right angle, so when we load the balance equally on both sides, the force on the right rotates the bar more strongly than the force on the left. The balance moves towards horizontal. It works exactly the same way if the left side is higher.
But we can get another fact very easily. If we change the distance below the bar where we apply the force,
the difference between the angles increases with the distance. The force towards horizontal on an equally loaded balance increases with the distance between the crosspiece and the point where we apply the force. The larger that distance, the more mass we have to add to one side to stabilize the balance at some particular angle.
When we use a balance, we add or remove mass to make it as close to horizontal as possible. There is a minimum angle we can detect, so the precision of the balance is the largest imbalance of mass which tilts the balance less than that angle. So the precision of a balance increases as the point where we attach the mass gets closer and closer to the crosspiece. If we actually attach it in the middle of the crosspiece, the balance measures infinitely small (i.e., no) deviation, and we can stabilize it at any angle we like. This is the naive case at the beginning.
The force rotating the balance around the pivot decreases well, though, so the instrument responds more and more slowly to changes in mass. Any real balance has to be a compromise between being able to use it in a reasonable amount of time and having sufficiently high precision for the task at hand.
Let’s summarize: when does a pivoting crosspiece act as a balance? When it is equally loaded, and placed at an arbitrary angle, there must be a force rotating it back to horizontal. This happens when the angle between force and the line from pivot to the point where the force is applied is closer to a right angle on the side that is up than on the side that is down.
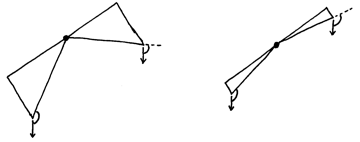
Exercise for the reader: Say whether each of the following devices with identical crosspieces and bases, differing only in the points of attachment of the mass, can be used as a balance. The pivot is marked as a black dot, the points where the mass is attached as white dots. Gravity always points towards the bottom of the page.