Type driven design

Status: Finished
Confidence: Likely

Let’s take two types and three functions. The types are Float and Integer. The functions are:

round : Float -> Integer  
jitter : Integer -> Float  
increment : Integer -> Integer  

We can draw a directed graph with the types as nodes and functions as labelled edges between them, pointing from input type to output type.

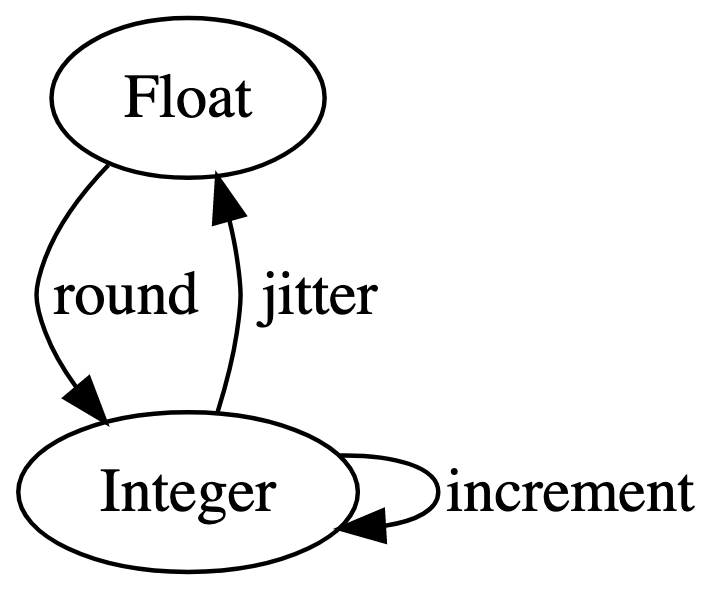
The input and output types of the functions mean that we can only chain them in certain orders. The following expressions all work

let i : Integer  
let x : Float  
  
jitter(increment(i))  
jitter(round(x))  
increment(round(x))  

and of course any number of increments inserted anywhere that we have an integer as input. These expressions don’t work:

round(increment(i))  
increment(jitter(i))  

On the graph above, there is no path we can follow that corresponds to those.

Mathematicians study this kind of object a lot under the name of category theory, but there’s an important difference between the graphs that mathematicians are interested in and the ones that programmers are interested in. Mathematicians wants graphs that are as general as possible, with the most possible paths and the most structure. They’re studying that structure and if there’s no much structure it’s boring. Programmers are trying to write programs. Only one path through all graph corresponds to the program I am trying to write, so programmers want to work with graphs with as few different paths, and as little interesting structure, as possible.

Let’s take an example of using this kind of graph to plan a program. Say that we have a JavaScript object that we want to redact. If we wrote this down only with reference to the values themselves, we are trying to write a function redact : Object -> Object. The corresponding graph is

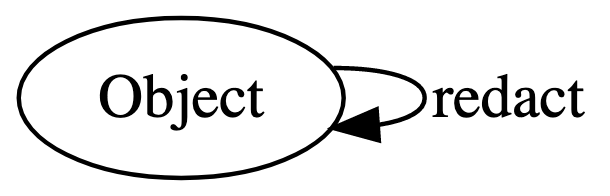
That graph doesn’t distinguish between unredacted an redacted objects, and for one node there’s a maximal amount of structure (we can redact and redact again, redact three times, etc.). This brings us to our first trick: separate values with different properties into different types, even if they’re represented in your language by the same type.

The input and output of redact are both objects, but in our mind we label them as “unredacted object” and “redacted object.” So let’s label them that way at the type level, even if, in the actual program, they are both JavaScript objects. Now we have

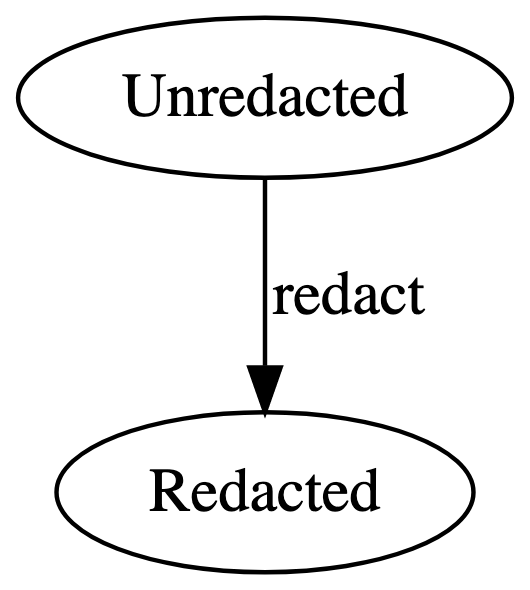
Now we’re getting somewhere. There’s only one program to be made from this graph, corresponding to the one path.

We still haven’t produced an actual program for redact, though. So let’s figure out how to do that. AWS has a service called Comprehend that will redact things for us.

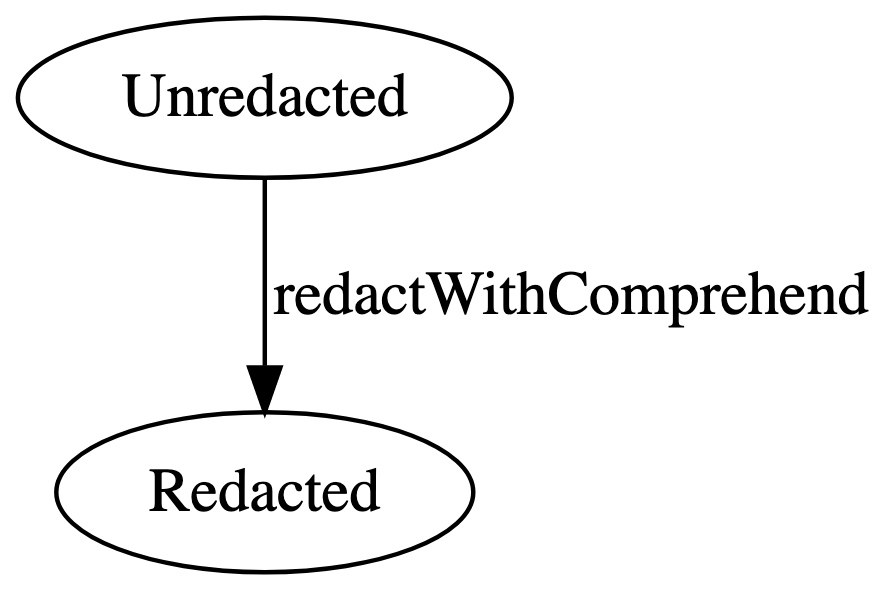
We may not want to redact all the data with Comprehend, though. In that case we need to insert a step that removes data we don’t want to send to Comprehend.

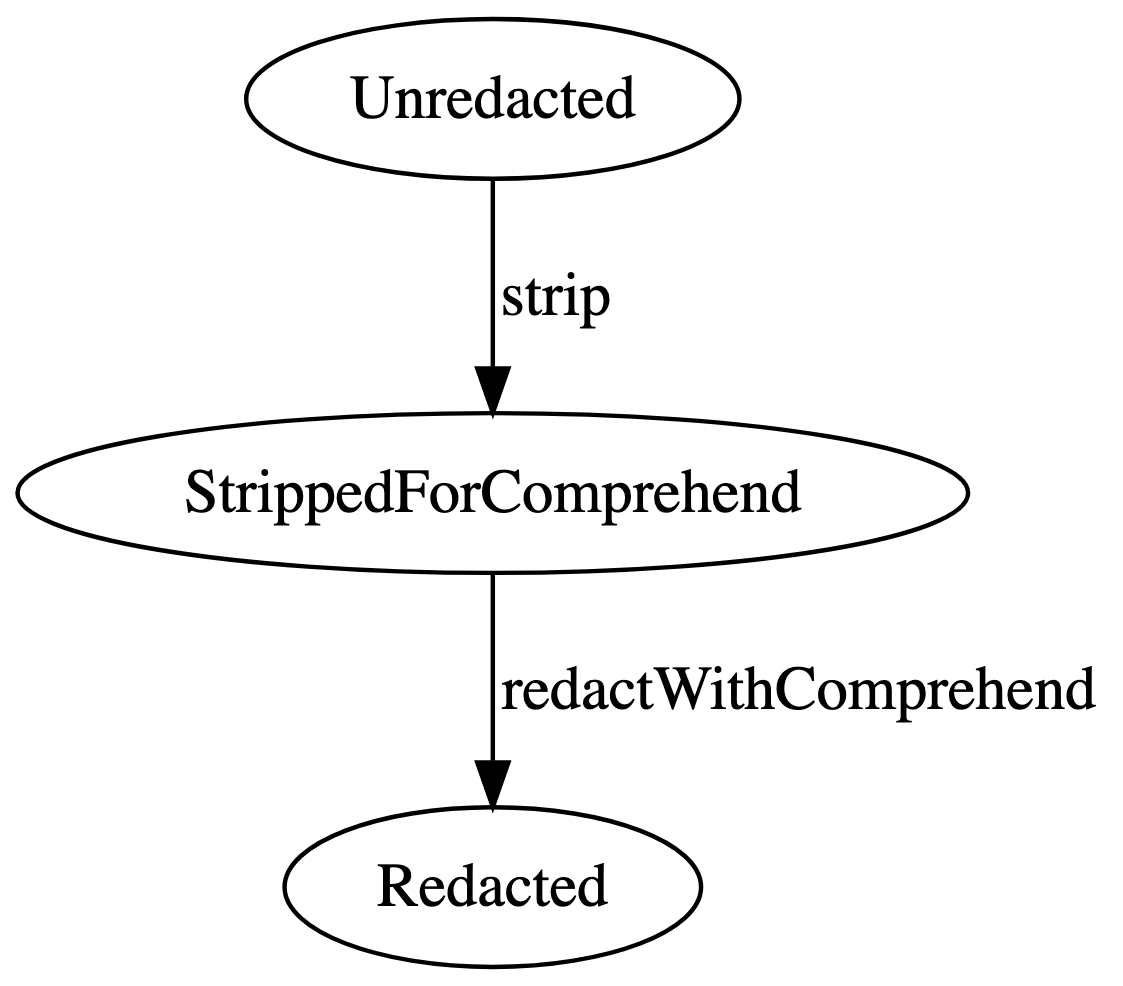
These are functions that I think I could actually write. But we probably don’t want to lose that data we aren’t sending to Comprehend. So we had better carry it through somehow. The diagrams start getting a little weird here, but bear with me. We’re going to introduce compound types. For simplicity we’re just going to introduce tuples. Instead of a function strip, we want a function split that takes an Unredacted and returns a pair (NotForRedaction, StrippedForComprehend). Now we have to add pairs of types to the graph, and edges between nodes that correspond to operating on those pairs. We also need a function to recombine the data.

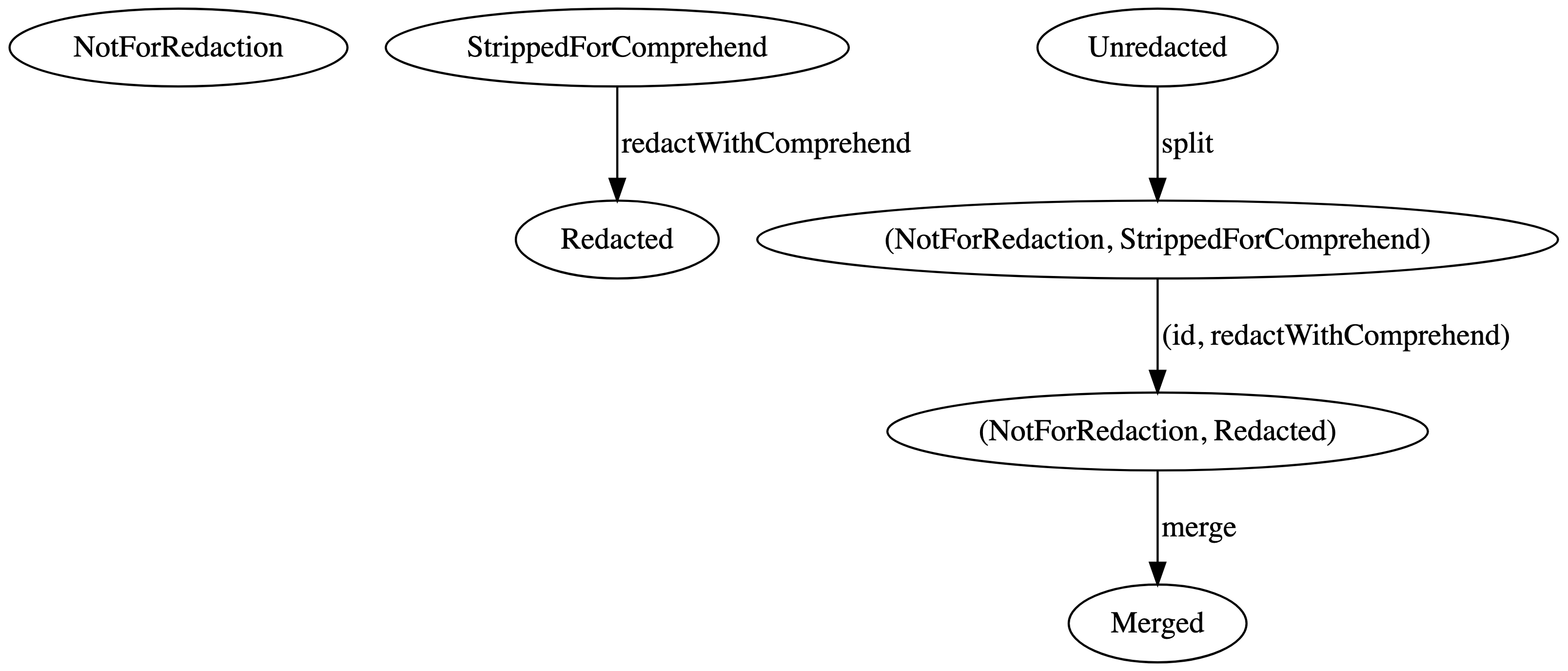
There is one path we care about here that begins with Unredacted and ends with Merged. The pair notation can be obscure, so it may help to draw that single path as a graph with splits and merges shown as separate paths

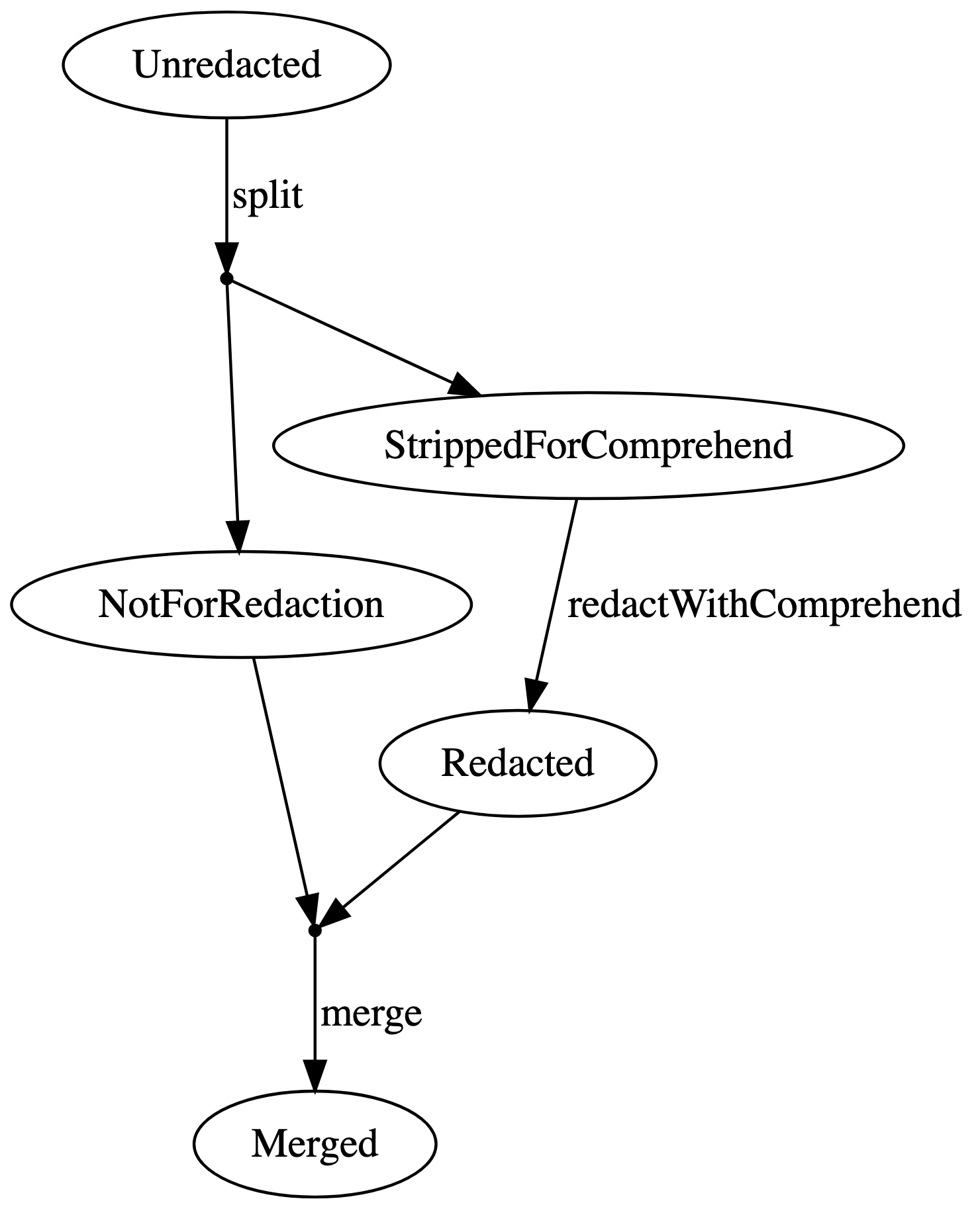
If we are designing our types so that we only have one or two paths, we can often get away with just drawing these diagrams instead of the proper diagram with tuples.

Comprehend has a limit on the size of the data it will accept from one request, so we will need to chunk our data, run Comprehend on each chunk, and then reassemble it. We can refine our diagram further to reflect that.

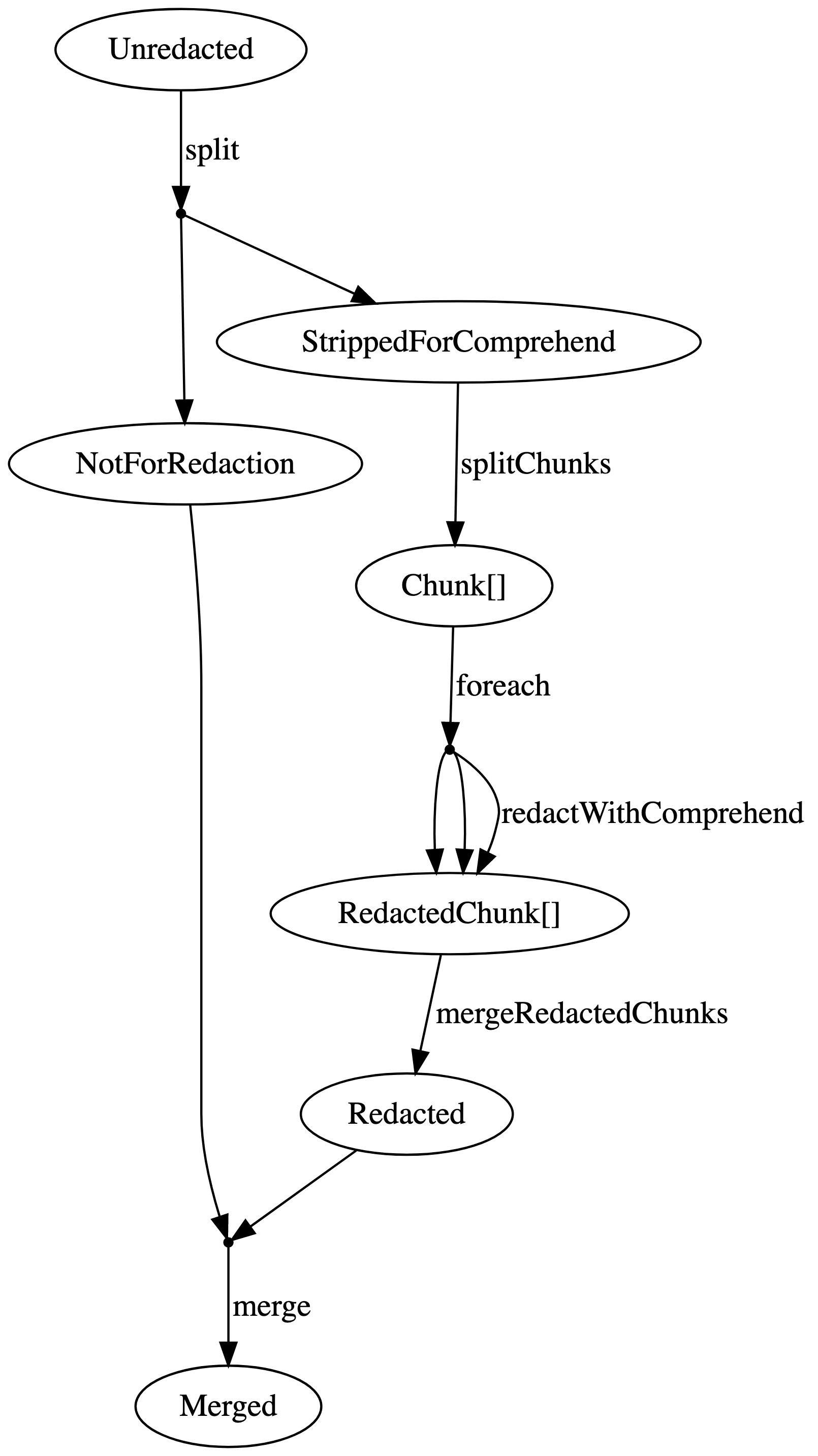
Each of these functions is one that we can probably write, with a clear contract on its input and output. We can almost read the main function definition off the graph:

def redact(input):
    (not_for_redaction, stripped_for_comprehend) = split(input)
    redacted_chunks = []
    for chunk in split_chunks(stripped_for_comprehend):
        redacted_chunk = redactWithComprehend(chunk)
        redacted_chunks.append(redacted_chunk)
    redacted = mergeRedactedChunks(redacted_chunks)
    return merge(not_for_redaction, redacted)

The graph is minimally structured. We have only one path through it from our desired input to our desired output. And every step we made was a successive refinement on one piece of the graph that we knew could not interact with any other piece, since there was no way for the types to match up.

« Back to Programming | Home