Measuring pointiness of functions

Status: Done

Math in this page not rendering? See the fix

Naively, it seems unlikely that an approximation by smooth functions like polynomials or complex exponentials can reproduce points and jags in the original function. As it turns out, it can, if the points aren’t too pointy. How do we measure “pointiness?”

Consider the family of functions $f_{k}(x)=1-|2x-1|^{1/k}$. The first few of these look like:

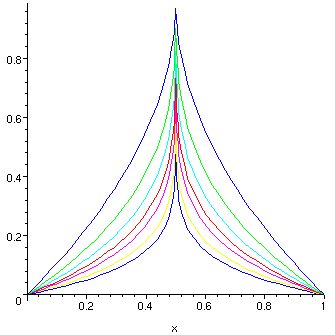
At $x=\frac{1}{2}$, these functions are obviously not differentiable, that is

$$\lim_{\varepsilon\rightarrow0}\frac{f_{k}(x+\varepsilon)-f(x)}{\varepsilon}$$

does not exist. The difference in the numerator doesn’t shrink fast enough to keep up with $\varepsilon$ in the denominator. But what if we slow down the denominator? The easiest way is to raise $\varepsilon$ to some power less than 1. So take

$$\lim_{\varepsilon\rightarrow0}\frac{f_{k}(x+\varepsilon)-f(x)}{\varepsilon^{\alpha}}$$

where $0\leq\alpha\leq 1$. If we put in a sufficiently small $\alpha$, then the limit may exist.

The $f_{k}$’s are smnooth everywhere except at $x=\frac{1}{2}$. Consider our new, slowed limit there.

$$\lim_{\varepsilon\rightarrow0}\frac{f_{k}(\frac{1}{2}+\varepsilon)-f_{k}(\frac{1}{2})}{\varepsilon^{\alpha}} = \lim_{\varepsilon\rightarrow0}\frac{(2\varepsilon)^{1/k}}{\varepsilon^{\alpha}}$$

which exists when $\alpha < \frac{1}{k}$. To see more clearly what this means, consider the box $[x,x+\varepsilon]\times[f(x),f(x+\varepsilon)]$:

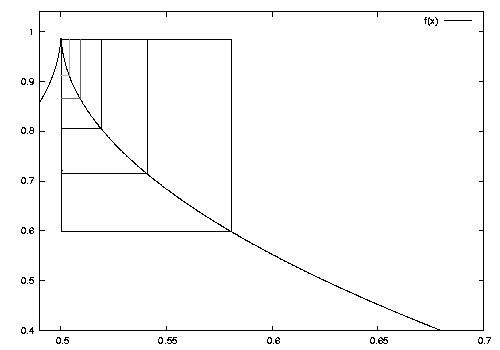
How much must we change $\varepsilon$ to half the height of the box? If the function is differentiable, the answer (eventually, for a sufficiently small box) is to halve the horizontal dimensions of the box as well, since all differentiable can be well approximated as linear on sufficiently small regions. For our $f_{k}$, we have to shrink $\varepsilon$ faster and faster as $k$ increases.

More generally, a function is said to be $\alpha$-Hölder continuous if $\alpha$ is the largest exponent in the denominator for which the limit above exists on the whole interval under consideration. The $f_{k}$’s provide a family of examples illustrating $\alpha$’s throughout the admissable range. $\alpha=0$ is discontinuous, and corresponds to $f_{\infty}$, which is a Dirac $\delta$ function. We can’t make the limit exist. Differentiable functions have $\alpha=1$.

This mostly comes up when you’re looking at Fourier analysis, where the theorem I learned is that partial Fourier sums converge at least where $\alpha \geq \frac{1}{2}$. For rougher creatures, the series may behave itself or not.

« Back to Miscellany | Home