The unit circle deformed

Status: Done
Confidence: Certain

Math in this page not rendering? See the fix

The distance between two points $x=(x_1,x_2,\dots,x_n)$ and $y=(y_1,y_2,\dots,y_n)$ in the classical Euclidean sense is

$$\| x - y \| = \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2 + \dots + (x_n - y_n)^2}$$

However, other measures are possible. On a grid (say, the distance to get from place to place in New York City), the distance is the lateral distance, since you can’t go on diagonals:

$$\| x - y \| = |x_1 - y_1| + \dots + |x_n - y_n|$$

We can dream up scenarios in which we take the cube of each term, and the cube root overall, or any other power that we care to choose. We’ll generalize, and define the $p$-norm of a vector $x$ to be

$$\|x\|_p = (|x_1|^p + \dots + |x_n|^p)^{\frac{1}{p}}$$

After you play with this for a while, you might ask, “what does the unit circle look like for some $p$?” We’ll explore this in two dimensions where it’s easy to see. Nothing new happens in higher dimensions.

$p=2$ is our usual norm, and the unit circle is our usual circle. If we go to $p=1$, our grid norm above, then we are plotting the equation $|x_1| + |x_2| = 1$ which is just four line segments connecting the points (1,0), (0,1), (-1,0), and (0,-1). The unit circles for $p=1,2,3,4$ look like

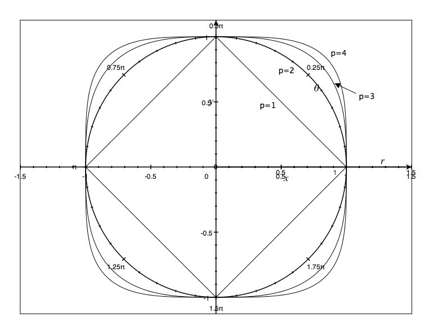
To see the more general behavior, note that we can take the norm of a fixed vector $x$ as a function of $p$. If we fix $x=(1,0)$, or any of the other points on the axes, then the norm doesn’t vary with $p$—it’s always 1. If we go at forty five degrees between the axes ($x=(1/\sqrt{2}, 1/\sqrt{2})$), then we have

$\|x\|_p$
$= (\frac{1}{\sqrt{2}^p} + \frac{1}{\sqrt{2}^p})^{\frac{1}{p}}$
$= (2\frac{1}{2^{\frac{p}{2}}})^{\frac{1}{p}}$
$= (2^{1-\frac{p}{2}})^{\frac{1}{p}}$
$= 2^{(\frac{1}{p}-\frac{1}{2})}$

This function looks like

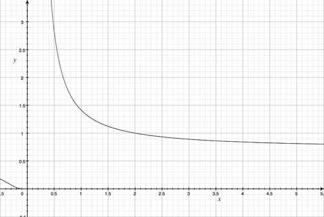
Remember, we have here a fixed vector: its value goes down, so in order to get a length of 1, we have to put in a longer vector. The unit circle thus heads steadily towards a square.

The limiting case is the $\infty$-norm, which is simply defined as $\|\mathbf{x}\|_\infty = \textrm{max}_i |x_i|$, the largest component of the vector. A few moments thought show that the unit circle is simply the square centered at the origin with side length two, and all sides parallel to the axes.

Given these insights into the unit circle, we can actually use this to get another characteristic of a vector. How much does it lie on the axes? Are only two of its components in this basis important? Three?

To measure this, consider our vector $\mathbf{x}$. Take

$$-\frac{d\|\mathbf{x}\|_p}{dp}|_{p=1}$$

What is this horrible object? Consider a simple case, where $\mathbf{x}$ has $k$ components which are 1 and $n-k$ components which are 0. Then

$- \frac{d\|\mathbf{x}\|_p}{dp}$
$= -\frac{d}{dp} k^{\frac{1}{p}}$
$= \frac{1}{p} k^{\frac{1}{p}} \log k^{\frac{1}{p}}$

When we evaluate this at $p=1$, we get $-d\|\mathbf{x}\|_p/dp|_{p=1} = k\log k$, which is at least monotonic in $k$, and gives us an estimate of the number of components.

« Back to Miscellany | Home